Partie A : pendule simple.

On étudie un pendule simple constitué d’une masse ponctuelle m, attachée à l’une des extrémités d’un fil inextensible, de masse négligeable et de longueur L.
Ce pendule est placé dans le champ de pesanteur dans
le référentiel terrestre considéré comme galiléen.

L’autre extrémité du fil est attachée en un point fixe A. Écarté de sa position d’équilibre G₀, le pendule oscille
sans frottements avec une amplitude .
G_i est la position initiale à partir de laquelle le pendule est abandonné sans vitesse.
Une position quelconque G est repérée par 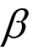, élongation angulaire mesurée à partir de la position d’équilibre.

• Étude énergétique.
  
  Donner l’expression de l’énergie cinétique en G.
  On prendra l’origine des énergies potentielles en G₀, origine de l’axe des z. On montre que, dans ce cas, l’énergie potentielle en G peut se mettre sous la forme :

E_p = mgL(1 – cos) .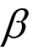

Donner l’expression de l’énergie mécanique en fonction de m, g, L, v et .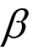
Pourquoi l’énergie mécanique se conserve-t-elle ?

• Exploitation.

Exprimer la vitesse au passage par la position d’équilibre en fonction de g, L et . Calculer sa valeur.
Données :  g = 10 m.s^-2 ; L = 1,0 m ; cos = 0,95.

Partie B : oscillateur élastique.

Un solide (S) de masse m, de centre d’inertie G, peut glisser sans frottements sur une tige horizontale. Il est accroché à un ressort (R) à spires non jointives, de raideur k = 4,0 N.m^-1. L’ensemble constitue un oscillateur élastique horizontal, non amorti.
La masse du ressort est négligeable devant m et (S) entoure la tige de telle sorte que G se trouve sur l’axe de celle-ci (voir schéma page suivante).
On étudie le mouvement de translation du solide (S) dans le référentiel terrestre supposé galiléen.
Lorsque le solide (S) est à l’équilibre, son centre d’inertie G se situe à la verticale du point O, origine de l’axe des abscisses. Le solide est écarté de 10 cm de sa position d’équilibre et abandonné sans vitesse initiale à la date t = 0 s.

Dispositif expérimental :

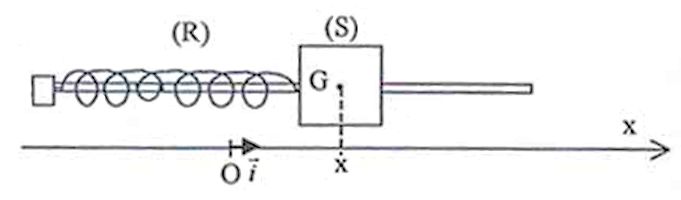
On procède à l’enregistrement des positions successives de G au cours du temps par un dispositif approprié. On obtient la courbe ci-dessous :

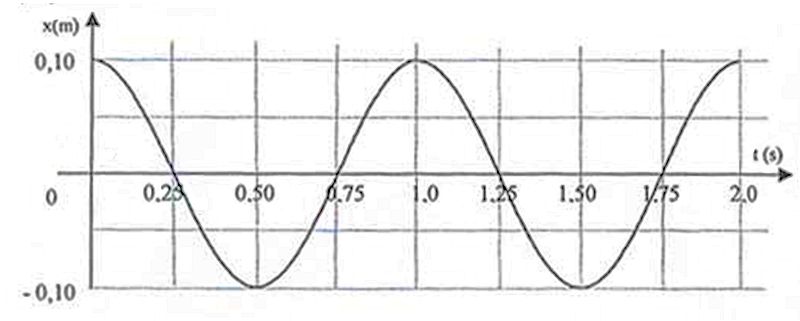
2. Étude énergétique.

L’énergie potentielle de pesanteur est choisie nulle dans le plan horizontal passant par G.

2.1. Donner l’expression littérale de l’énergie mécanique du système {ressort + solide}, en fonction de k, m, x.
2.2. À partir de l’enregistrement ci-dessus, trouver pour quelles dates l’énergie potentielle élastique du système {ressort + solide} est maximale. Que vaut alors l’énergie cinétique ?
2.3. Calculer la valeur de l’énergie mécanique du système.

Partie C : comparaison des périodes.
Les comportements des deux pendules précédents sont maintenant envisagés sur la Lune.

Expression de la période du pendule pesant :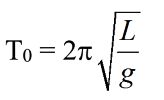

Expression de la période du pendule élastique :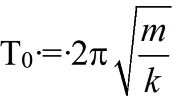

Parmi les hypothèses ci-dessous, choisir pour chaque pendule celle qui est correcte. Justifier.

Les trois records de Félix Baumgartner

Extrait du texte introductif :

Le 14 octobre 2012, Félix Baumgartner a réalisé un saut historique en inscrivant trois records à son tableau de chasse : celui de la plus haute altitude atteinte par un homme en ballon soit 39 045 m d’altitude, le record du plus haut saut en chute libre, et le record de vitesse en chute libre
soit 1341,9 km.h^-1.

La masse de Félix Baumgartner et de son équipement est m = 120 kg.

L’intensité du champ de pesanteur est considérée comme constante entre le niveau de la mer et l’altitude de 39 km : g = 9,8 m.s^-2

2.3. Calculer la variation d’énergie mécanique entre le moment où Félix Baumgartner saute et le moment où il atteint sa vitesse maximale. Interpréter le résultat.

2.4. Analyse de schémas. (non étudiée ici).

2.5. v = 8,8 m.s^-1 valeur calculée nécessaire à la résolution de la question 2.6. (non étudiée ici).

2.6. Pour acquérir la même vitesse à l’arrivée au sol, de quel étage d’un immeuble Félix Baumgartner auraitil dû sauter ? Commenter